When playing a kahoot with a brainstorm question, participants can enter ideas of arbitrary length, which are efficiently packed and visualised as cards on the host screen in the following way:
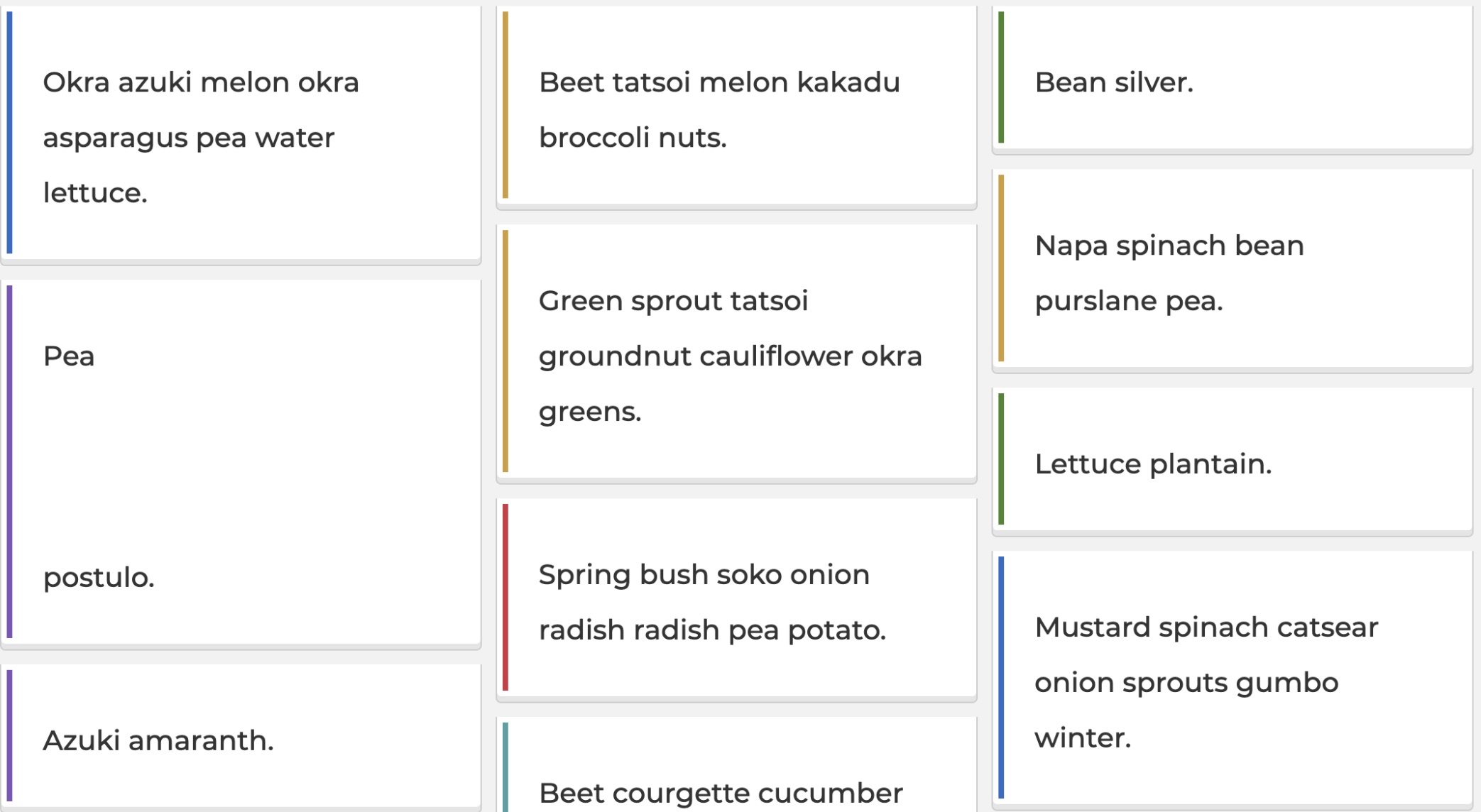
The arrangement of these answers is dynamic and cannot be pre-determined. But we wanted to add a number to each answer, so that the host and audience could get a better overview and refer to the answers by their numbers.
Have a look at the above image. How would you assign numbers to these cards?
The Goal
We wanted to implement a numbering system that would fulfil two criteria:
- Determining the numbers cannot be too slow, e.g. quadratic complexity. We can have up to 2000 answers and they need to be swiftly re-enumerated when the layout changes due to drag and drop
- The numbering should follow a natural left-to-right flow. We’ll try to refine this criteria more later.
Initial attempt
Let’s have a look at a basic attempt.
- Sort the answers by their position, where the y position matters much more than x. This is similar to how the masonry layout works in the browser (at the time of writing, only available in Firefox).

The easiest way to grok this is to visualise a slanted line coming in from above. When the line touches a card, it gets enumerated:

This is a good start, but not ideal. The second row goes backwards (6, 5, 4). We can amend this problem by changing the angle of the line, but that doesn’t generalise too well in different scenarios. Let’s look at the result so far and try to identify the problem:
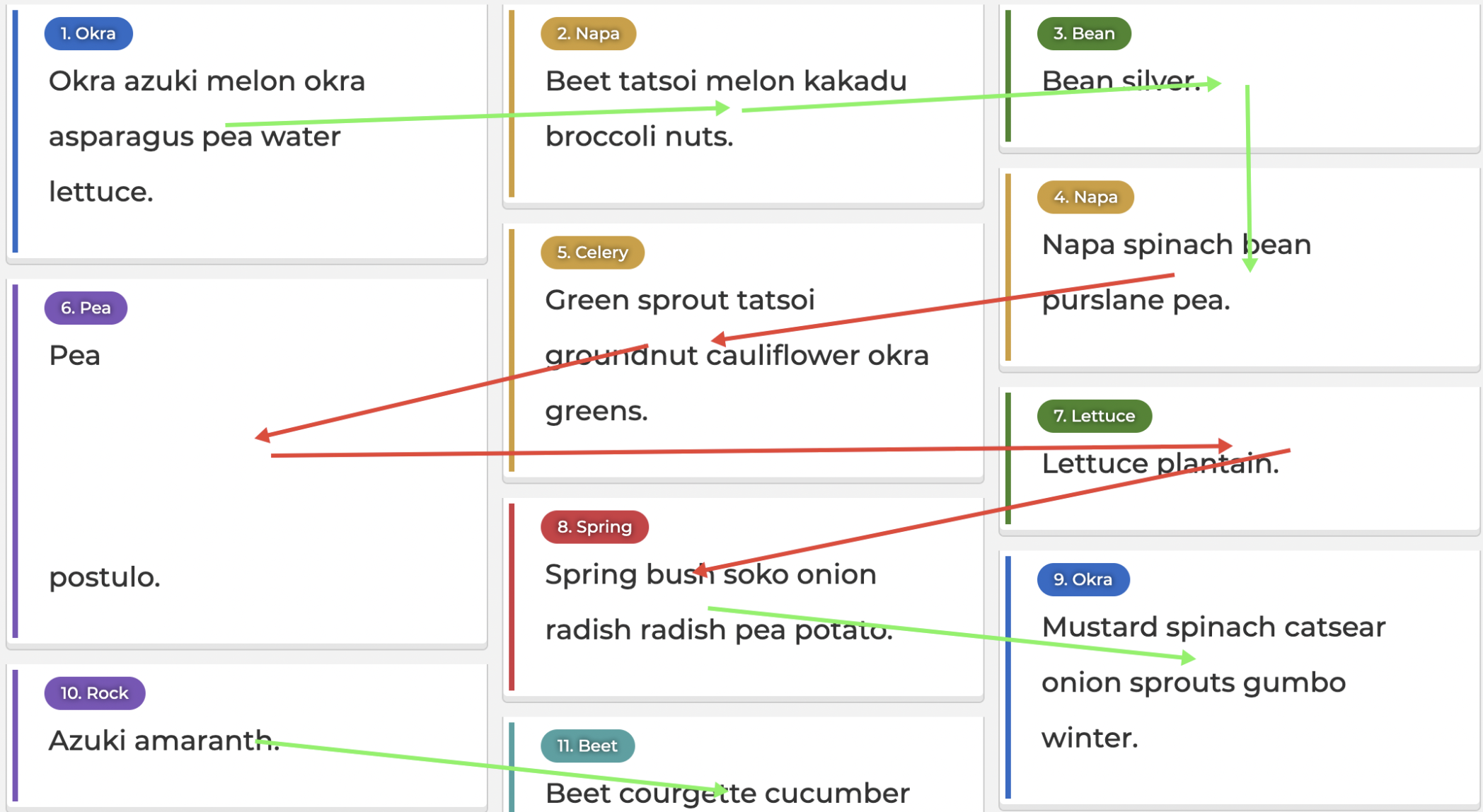
The order frequently goes against intuition, as annotated here with the red arrows.
The Basic Approach
From here, we’ll construct an algorithm with the following steps:
- Sort the cards by their position as demonstrated above.
- Go through the list of cards once again and try to improve the result by making small swaps between neighbouring cards.
This saves us from the quadratic performance drain of the “compare everything with everything” approach. The sorting implementation is probably not more than ?(n*log(n)), and the second step only adds one more traversal, so step 2 is only ?(n).
Let’s see how we can swap cards successfully.
- For each card, get the (number of columns + 1) next cards. (3 + 1 = 4, in this case)
- Determine which card has the minimum distance to the current card.
- That card will be the next one. If that was not the expected card from the sorting step, perform a swap.
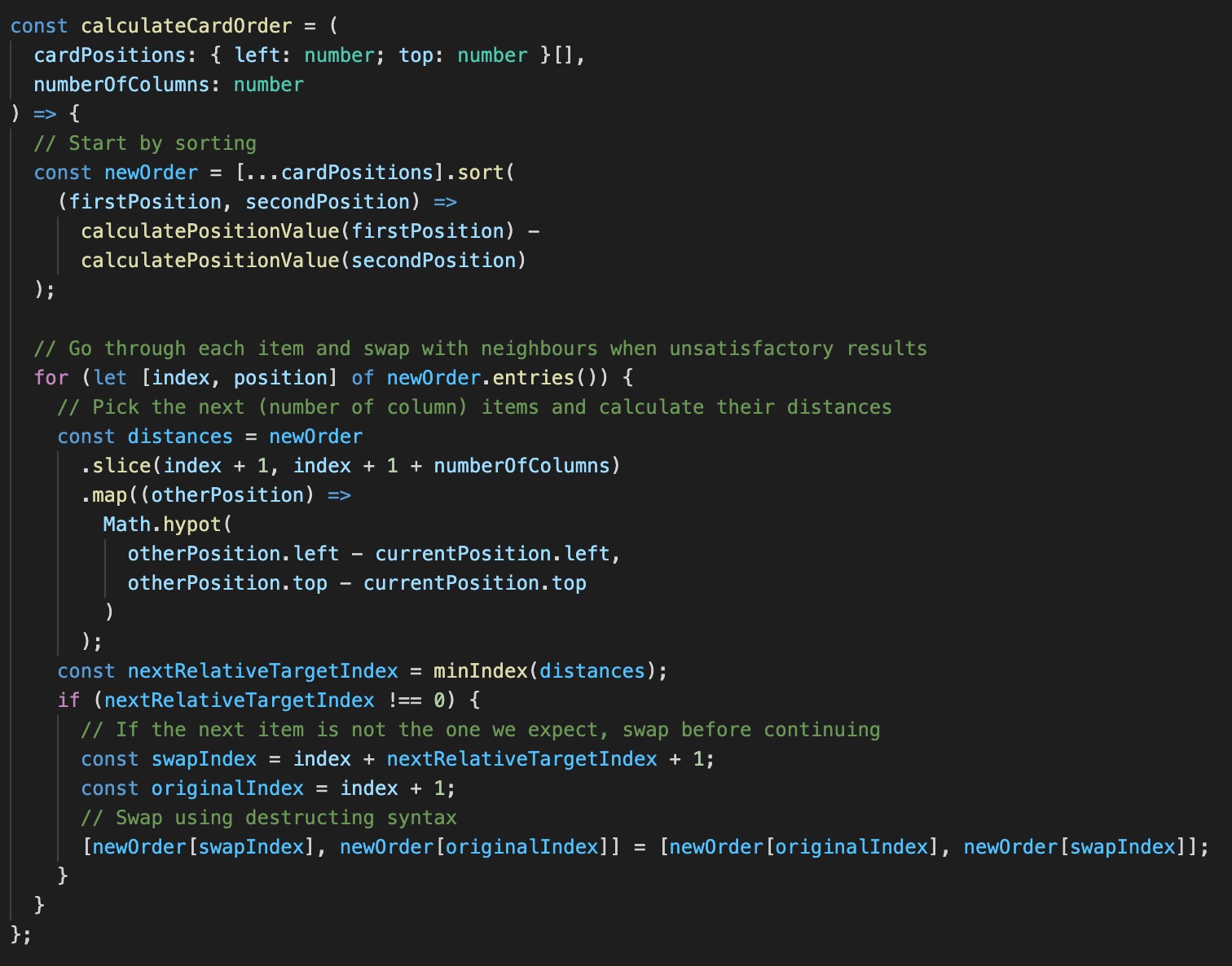
The function minIndex gets the index of the smallest value of an array of numbers, and is left out for brevity. However, this doesn’t quite work yet. Let’s have a look why, by imagining how this would play out for card number 2:
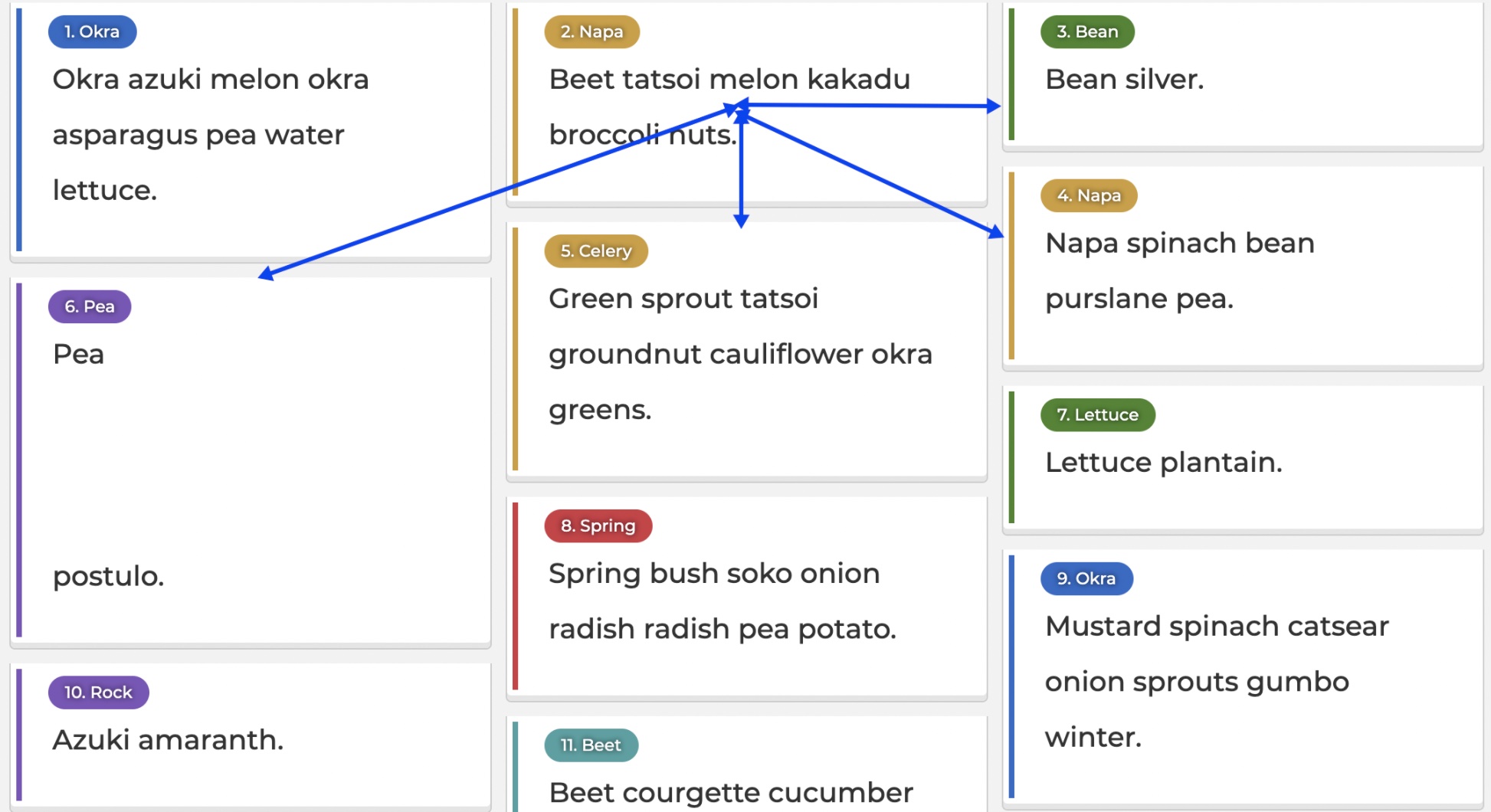
The distances are visualized as blue arrows here. The shortest one is to number 5, but we don’t want a jump down from 2 to 5. Also, going to number 6 should be more discouraged since we’re moving backwards. Let’s refine it a little bit:
- Cards to the left should not go backwards in the x-axis, but instead wrap around as if positioned further to the right
- When calculating the horizontal distance, earn the first column to the right “for free”. This incentivises traversing to the right instead of downwards.

In the image below, the x distance we gain “for free” is annotated in grey:
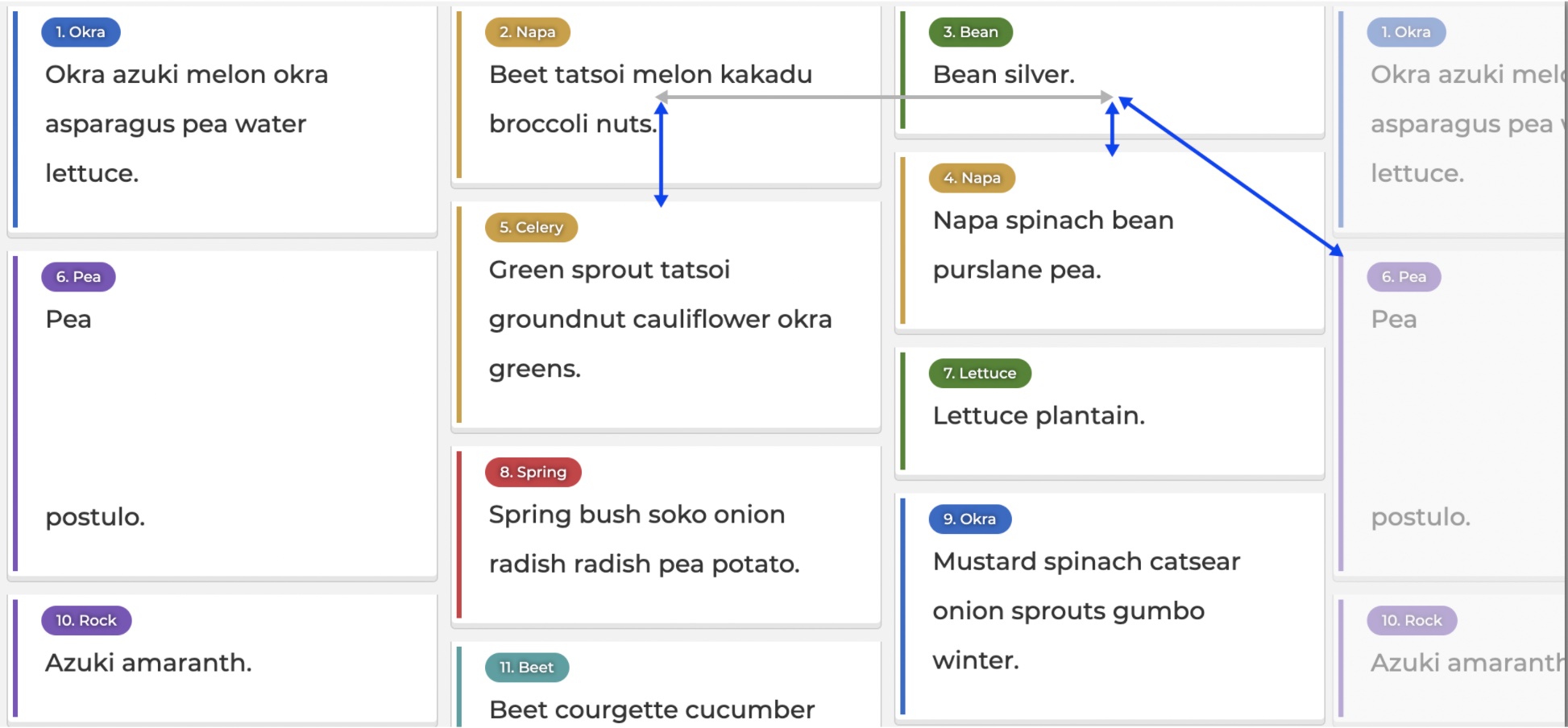
It works and successfully goes from 2 to 3. And look what happens for card 4:
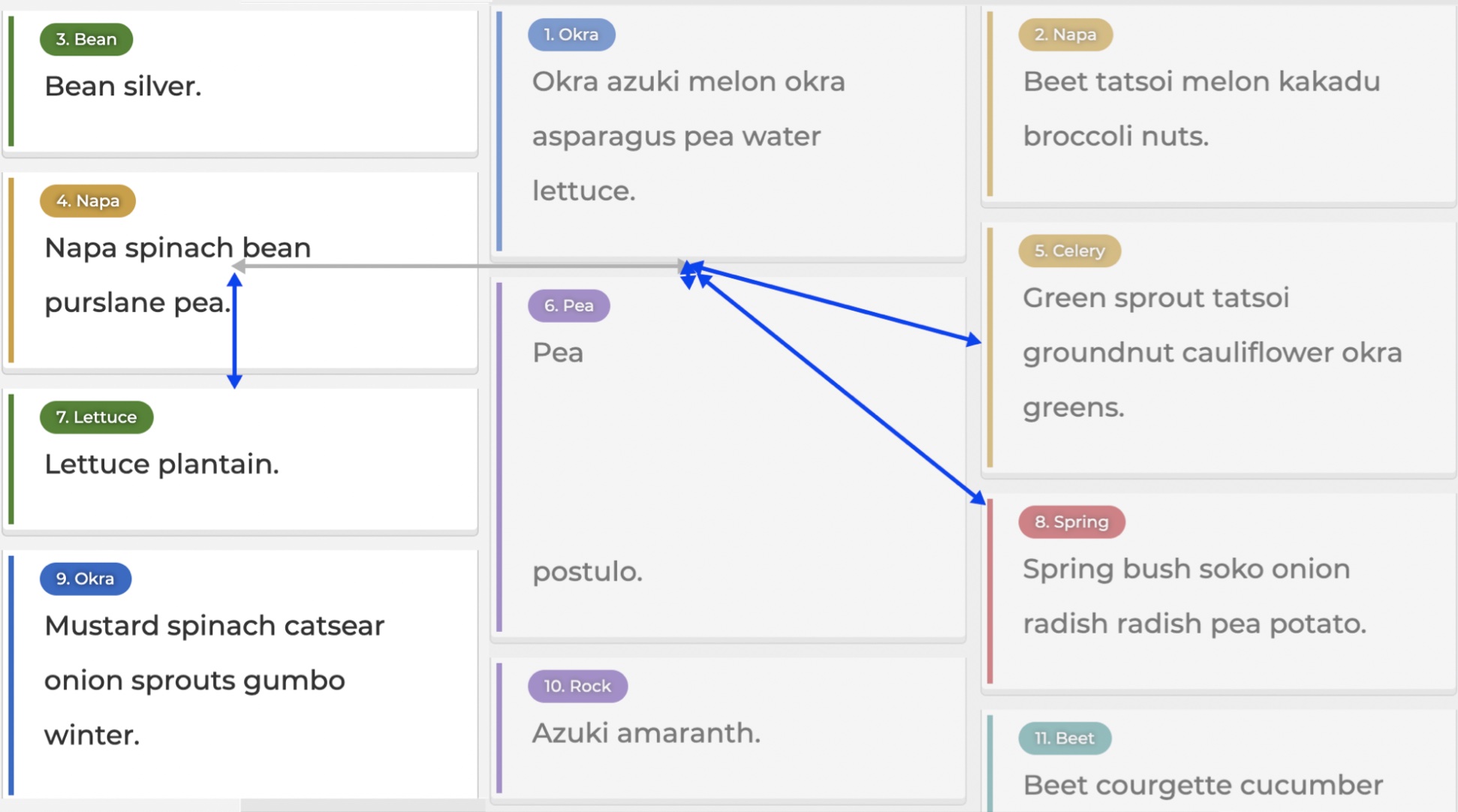
The distance to number 6 is shorter than 5, so there will be a swap. After all the swaps, the result looks like this:
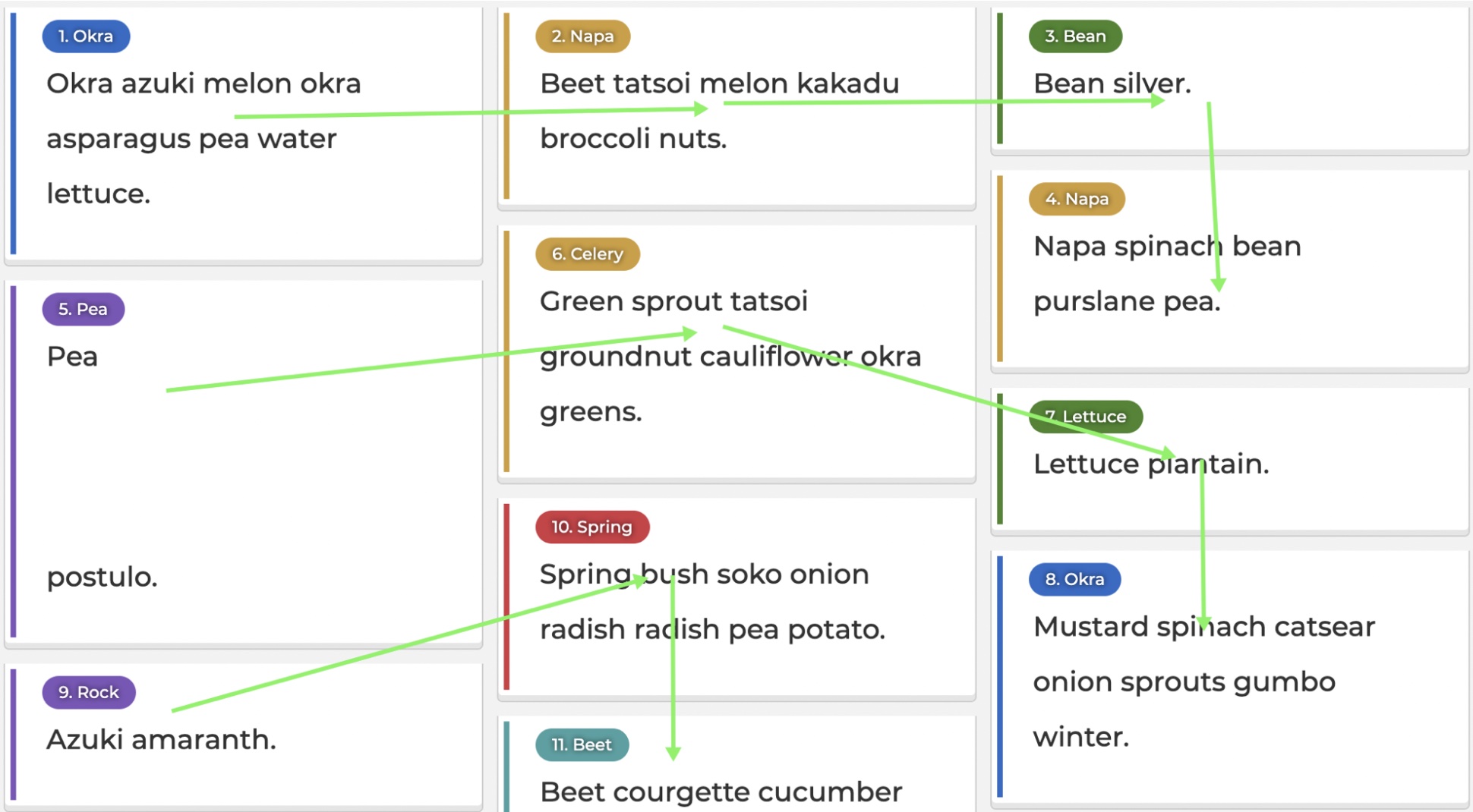
Much better.
Fine-tuning
We’re almost there. But the ordering on the last few cards doesn’t look great, so add one more case:
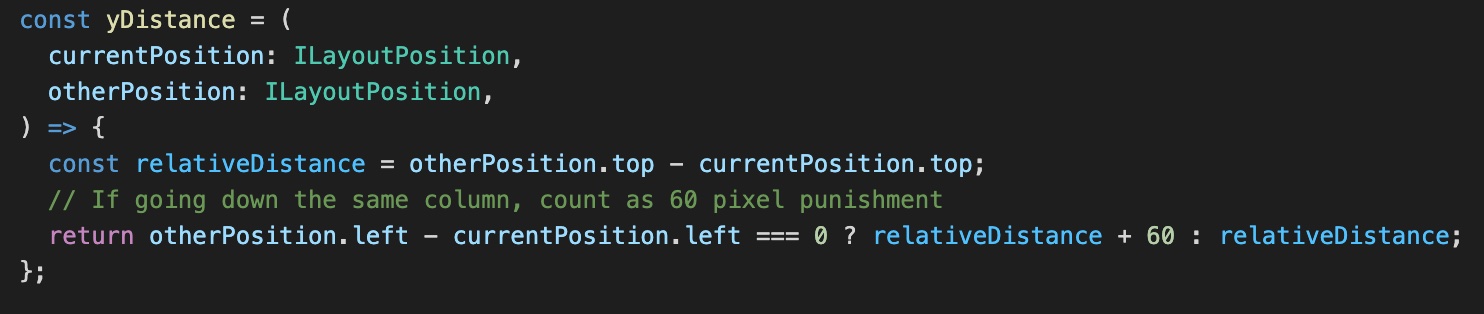
- When calculating the vertical distance, add an extra negative weight if the comparison card is directly below, in order to prevent from going down columns too easily.
It turned out that setting the negative bias value to 60 pixels gave a satisfactory result for a wide range of layouts.
It resolved the situation nicely:
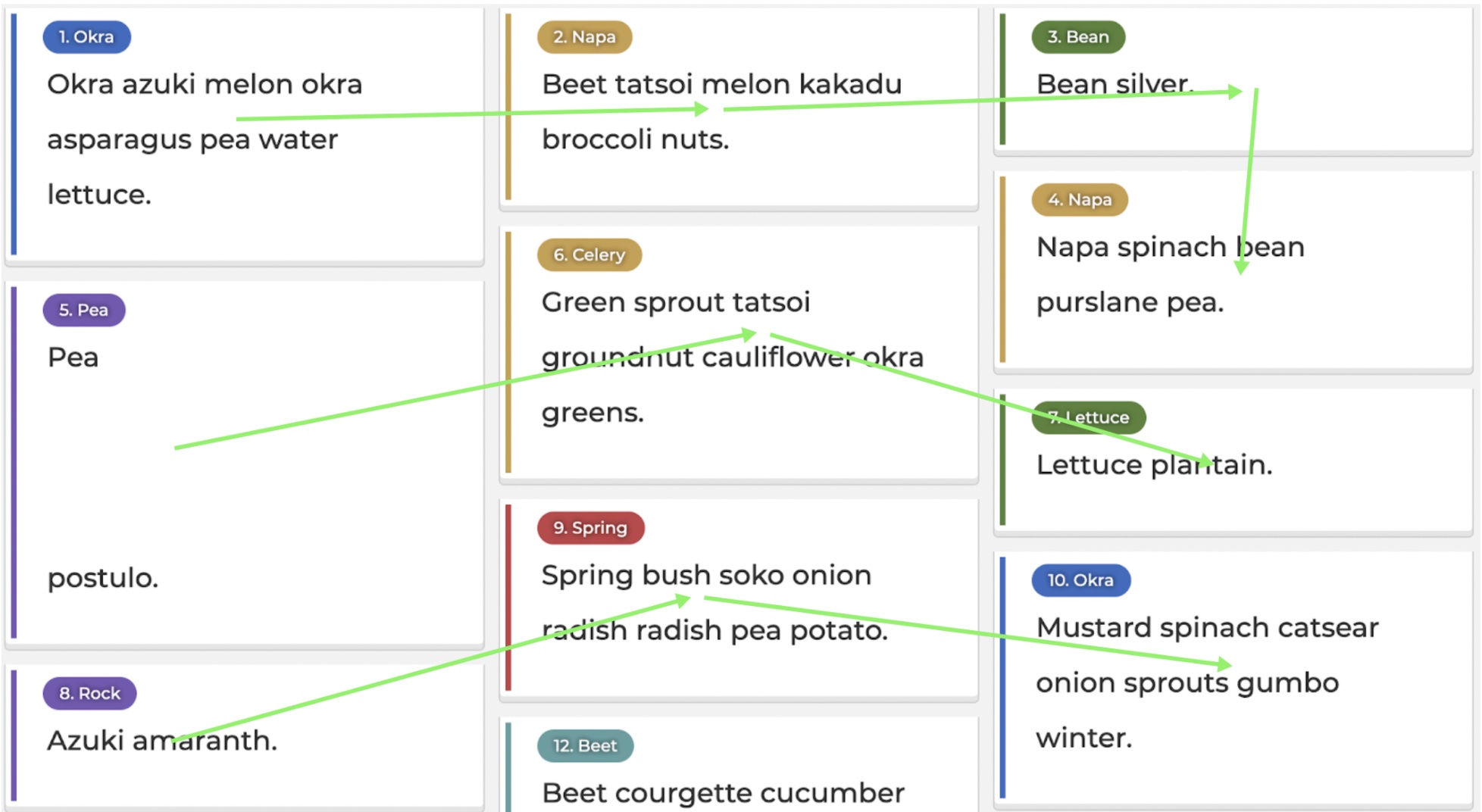
Conclusion
When facing a problem that lies off the beaten path, you should pick your battles carefully. In this case, the full code for solving the problem amounted to approximately 100 lines including comments, and was probably worth the effort. Frequent trial and error can be a great way to avoid diving too deep into rabbit holes.


